The first thing we need to establish to describe an orbit is a suitable inertial reference frame.  For our examples, we will confine ourselves to the bodies orbiting the earth and use the geocentric-equatorial system. This system has its origin at the center of the earth and its fundamental plane (XY plane) as the equatorial plane.

 

The Z-axis points in the direction of the north pole and the X-axis always points in the direction of the vernal equinox.  This means that this system does not rotate with respect to the stars and the earth turns relative to it. Three useful vectors are the I, J and K unit vectors which lie along the X, Y and Z axes respectively (as seen in the figure).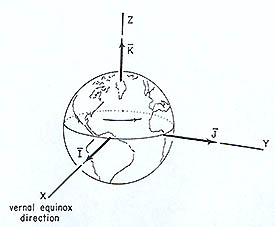

 

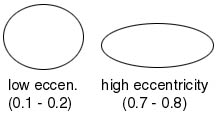
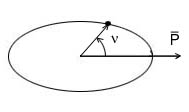
Now we can discuss the independent variables that are used to describe the orbit: the 'orbital elements.'  These six values are sufficient in describing the size, shape and orientation of an orbit as well as the exact position of the orbiting body.  The orbital elements are described below:

 

a, semi-major axis  (a constant describing the size of the orbit)	e, eccentricity  (a constant describing the shape of the orbit)	n, true anomaly (the angle in the plane of the satellite orbit between the direction of periapsis and the position vector of the satellite)

 

W, longitude of the ascending node, (the angle in the fundamental plane between the I vector and the point where the satellite crosses through the fundamental plane in the northerly direction)

i, inclination, (the angle between the K vector and the angular momentum vector h which is perpendicular to the plane of the satellite's orbit)

w, argument of periapsis, (the angle in the plane of the satellite's orbit, between the ascending node and the point of periapsis)

   

This information came largely from 'Fundamentals of Astrodynamics,' written by Bate, Mueller and White and published by Dover in 1971.

---

 

Introduction

Background

Basics

2D Viz

3D Viz

Tracking

Conclusions