As mentioned in the Basics Page, the orbit path is constrained to one plane called the ecliptic.  By just looking at the orbit in this plane, we can get a good picture of the size and shape of the orbit in relation to the planet about which it is traveling.  In order to visually explore the many different possible orbits, I wrote a small program in MatLAB. 

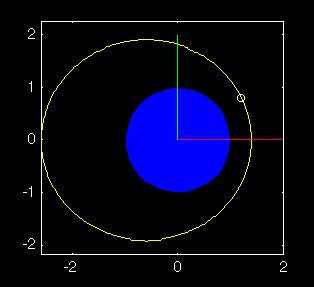
    This program prompts the user for 'a,' the semi-major axis, 'e,' the eccentricity, and 'n,' the true anomaly.  The user can also choose the default values (2, 0.3, and 33 respectively) by just pressing the enter key.  The first figure (as seen below) that is generated, contains an image of: the central planet (blue sphere), the orbiting body (small white circle) and its path (yellow), as well as the 'P' (red) and 'Q' (green) vectors. Length units in this figure are nondimensionalized with the planet's radius. 
 
 
 
    After the first figure is generated, the program pauses, and waits for the user to strike any key to continue.  Next, the program asks the user if they would like to see a plot of the velocity of the celestial body versus position in the orbit (second figure above).  The velocity is nondimensionalized and the position is in terms of true anomaly (0 - 360 degrees).  It can be seen that the body is traveling the fastest when it is closest to the planet at the 'perigee,' and the slowest at the 'apogee.' 

    To download this program click here: 'orbit.m'  In order to run this file, simply save it under the MatLAB directory on your hard drive and type 'orbit' at the MatLAB prompt.
  

 
Introduction Background Basics 2D Viz 3D Viz Tracking Conclusions