Surface Energy from Shear in the {1,1,2} Type Plane
in Body-Centered Cubic Iron

    Ductililty is a measure of a material's ability to deform plastically before failure occurs.  Engineers select and use a material in their designs partly on the basis of its ductility.  At an atomistic level, deformation behaviour is closely related to dislocation phenomena in material structures.  Therefore, an understanding of the ductile behaviour and the associated dislocation phenomena of materials is critical in the development and refinement of materials and in their use in engineering design.

    Dislocations move in two manners, glide or climb.  Glide motion occurs when atoms displace in the direction parallel to the plane containing the atoms.  Climb occurs when atoms displace in the direction perpendicular to the plane containing the atoms.  Glide of many dislocations is termed "slip".  Atoms creating a plane successively displace over a second plane.  These planes are called "slip planes".  This is the most common type of plastic deformation in crystalline solids.

    A characteristic shear stress is required to move dislocations.  After this characteristic shear stress is obtained, atoms are displaced from a reference state to a new state described by a vector called the Burgers vector.  The resulting relationship of slip planes gives rise to a surface energy g, or stacking fault energy.  Greater stacking fault energy results in a more unstable structure.

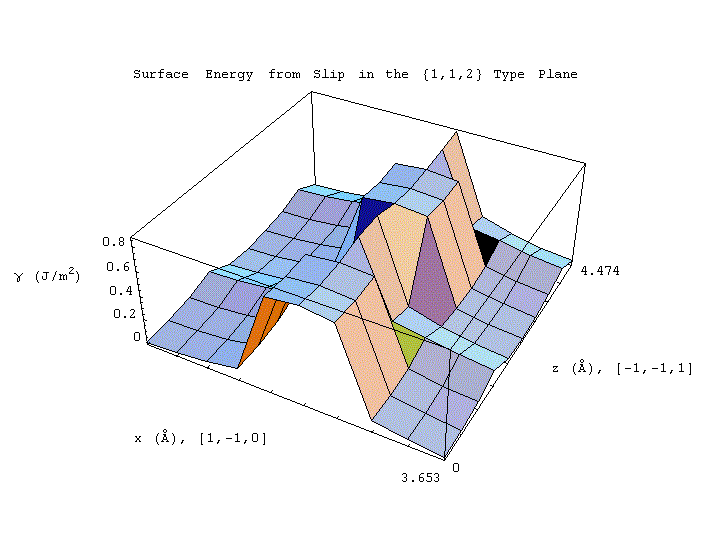
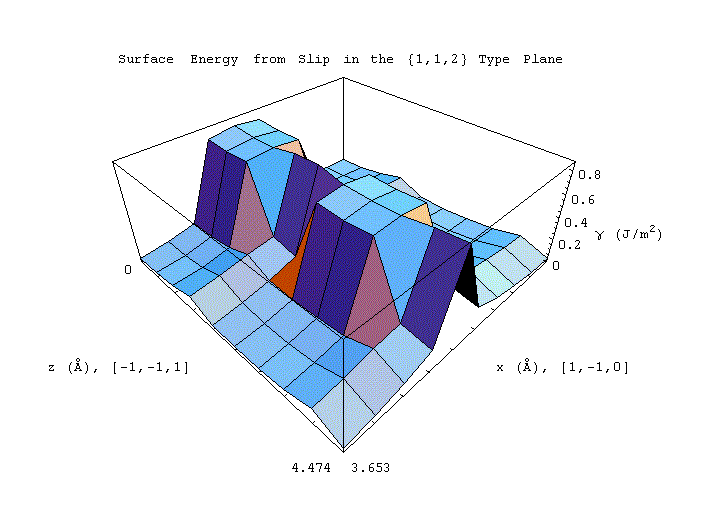
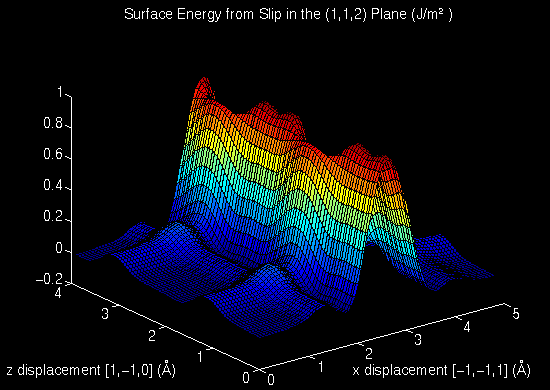
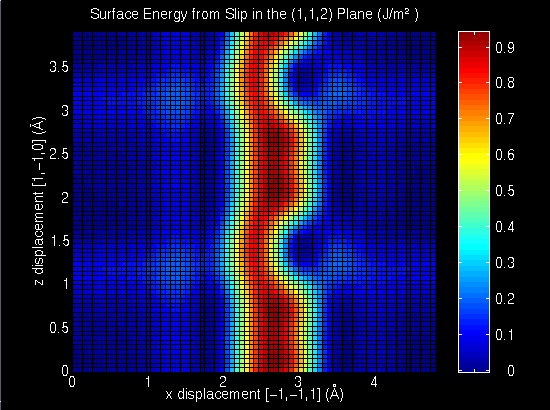
    In the study that follows, Conner, Van Looveren, and Bouthiette ran computer simulations to calculate surface energy resulting from variable slip in body-centered cubic iron.  Bcc iron has lattice parameter, a,  of 2.87 Angstroms and a cohesive energy of 6.86 x 10^-19 J.  Typical slip planes for bcc structures are {1,1,0},{1,1,2}, and {1,2,3}.  This study evaluates the {1,1,2} type plane.  In the simulation, the {1,1,2} plane contains the x and z axes, while the y axis is perpendicular to the plane.  A vector, having x and z components, assigns the conditions of the slip resulting from shear.  X values range from 0 to nine-tenths of the square root of two times the lattice parameter with intermediate values of n times one-tenth of the the square root of two times the lattice parameter.  Z values range from 0 to nine-tenths of the square root of three times the lattice parameter with intermediate values of n times one-tenth of the square root of three times the lattice parameter.  All possible combinations of x and z values are evaluated.  The resulting surface energies for variable slip in the {1,1,2} plane for body-centered cubic iron are tabulated below.

    Mathematical modeling software packages including Mathematica and Matlab aid in the visualization of the resulting surface energy data.  Surface plots and contour plots from Mathematica and Matlab are provided below.  The first two surface plots were completed using Mathematica.  The data was not interpolated resulting in the sharp edge forms.  The final surface plot and the contour plot were made using MatLab.  Data was interpolated.  The maximum surface energy is 0.847 J/m² for x equals 2.029 Angstroms and z equals 1.988 and 4.474 Angstroms.  Maximum surface energies for each z value tested occured for x equals 2.029 Angstroms.  The energies decrease symetrically moving away from the plane x equals 2.029 Angstroms in both directions along any constant z.  This symmetry is evident in all graphs.  Note that the combinations of x and z values with their corresponding surface energy values constitute a unit block that is repeated in all directions in the slip plane.
 

 

 

 

 
 

Works Consulted

Hull, Derek and Bacon, D. J. Introdution to Dislocations.  3rd ed.  New York:  Pergamon Press, 1984.

Callister, William D., Jr. Materials Science and Engineering, an Introduction.  4th ed.  New York:  John Wiley & Sons, 1997.