Jason A. Burdette
Assignment 3
ESM 4984
Simulation of Notch Impact Test on S-7 Tool Steel
This assignment involved the simulation of a notch impact test in which a pre-notched specimen of S7 Tool Steel was subjected to impact over a range of speeds. An existing simulation program, which accepted the material properties as well as the impact speed, was used and the results were analyzed by monitoring the time history of stress at key elements around the crack tip.
This information was used to determine the critical impact velocity for the material under these specific testing conditions. The critical impact velocity is the velocity at which the mode of failure transitions from brittle to ductile. The transition occurs because as the rate of loading is increased, the yield stress of the material actually changes. It increases as plastic strain increases and decreases as the temperature of the strained material increases. When the hardening and softening effects are equal, the material becomes unstable and a shear band develops.
This simulation uses these principles to determine the mode of failure of the material with specific material properties under specific loading conditions. The material parameters for S7 Tool Steel are shown below:
shear modulus G = 117 GPa
quasi-static yield stress A = 1.5389 GPa
strain hardening parameters B = 0.476
n = 0.18
strain-rate hardening parameters C = 0.012
m = 1.00
Tm = 1763 K
ambient room temperature Tamb = 298 K
The general location of the elements of interest is shown in Figure 1.

Figure 1: Elements of interest for pre-notched specimen (after deformation)
Impact speeds were varied from 10 to 60 m/s (in multiples of 10). For each impact speed, eight elements were analyzed for maximum principal stress and eight elements were monitored for Von Mises stress. Plots of these stresses over time for each element were generated and are included with the hard copy of this report.
The plots of maximum principal stress were used to determine the time to brittle failure by finding the time at which the first of the eight elements achieved 2.00 GPa. This value is somewhat arbitrary, as the assignment called for the time at which the first element achieved a principal stress equal to 2A or 3.08 Gpa for this material. Since this value was never achieved in my simulation, I chose 2.00 GPa, about 83% of the maximum stress achieved and an easy value to read from the charts. This time, tbrittle, was found for each of the impact speeds.
The plots of Von Mises stress were used to determine the time to ductile failure by finding the time at which the first of the eight elements reached 90% of the maximum Von Mises stress. Again, this time, tductile, was found for each of the six impact speeds.
Figure 2 shows the behavior of tbrittle and tductile over the range of impact speeds.
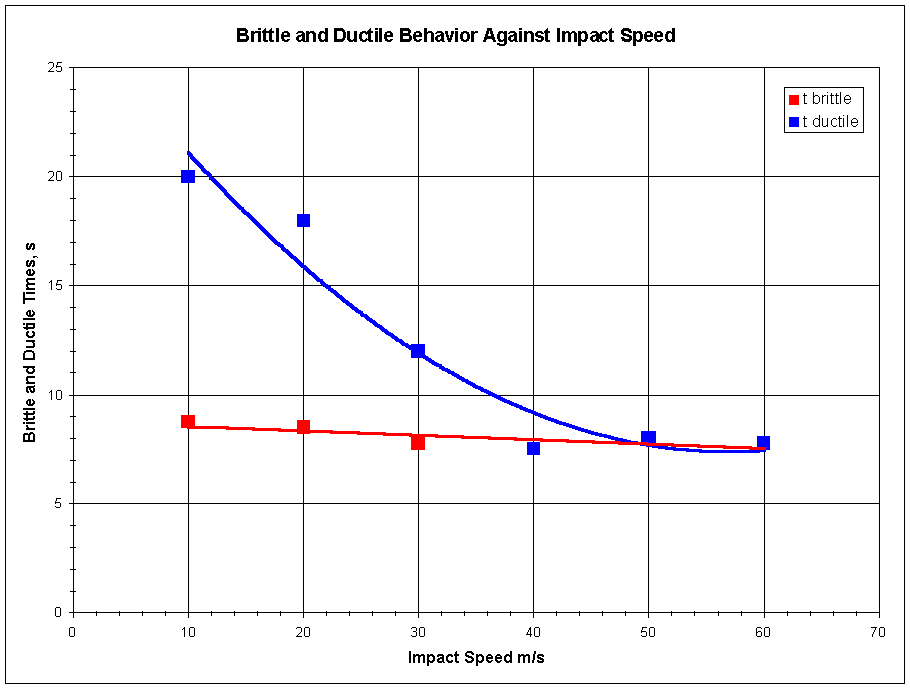
Figure 2: Brittle and Ductile Failure Times Over Range of Impact Speeds
The critical impact velocity is the velocity at which the mode of failure transitions from brittle to ductile. See that for low impact speeds, tbrittle is lower than tductile so brittle failure occurs before ductile failure. For this example, the intersection of the two curves is not clearly defined and therefore, the critical impact velocity not clearly defined. It appears to be in the range of 50 m/s, but scatter in the data as well as a leveling of both curves at higher impact speeds clouds this conclusion. It is possible that if I looked at a different stress from the arbitrary 2.00 Gpa, I would have been able to draw more certain conclusions.