Shows the data obtained from the tungsten analysis. All times are in m s. Dynamic Fracture of a Tungsten Plate
Christopher Bouthiette
MSE 4984
11/6/98
Tungsten is often referred to as a refractory metal. It has a very high melting temperature and consequently a very high elastic modulus. These properties lend it to be very useful as a penetrator in ballistic applications. The Johnson-Cook material model was used to model the material with the Dyna2D explicit finite element code. The Johnson-Cook model describes plasticity in metals under strain, strain rate, and temperature conditions.
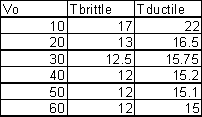
The problem posed was to impact a tungsten plate with an impactor at various speeds Vo. Six speeds were chosen 10, 20, 30 ,40, 50, and 60m/s. Depending on the speed the material should either fail through brittle fracture or through ductile fracture. The expected results would show that the slower speeds would fail in a brittle manner and the faster in a more ductile manner. This could be seen by plotting the times to brittle and ductile failure for the tungsten plate. The brittle curve would be a plot of time to brittle failure vs. Vo. Brittle failure is determined for the tungsten plate by when the max principal stress reaches 1.8Gpa. The ductile curve would be a plot of time to ductile failure vs. Vo. Ductile failure is determined for the tungsten plate by when the effective stress reaches 90% of Max stress. Vc is the point where the curves intersect.
Shows the data obtained from the tungsten analysis. All times are in m s.
My analysis of tungsten did not show an intersection of the curves. Brittle failure seems that it would occur faster in each of the cases. The plot of the two curves can be found on the next page. Four sample graphs can be found from the 20m/s case. A sample d2hsp file is also included to verify constants used in solution.
JOHNSON-COOK MODEL.SIMPLE TENSION.
material constants set number .... 1
material model ............. 12
equation-of-state model .... 1
hourglass control model .... 1
bulk viscosity model ....... 1
den .............................. = 1.7000E+01
hourglass coefficient ............ = 1.0000E-01
quadratic bulk viscosity ......... = 1.5000E+00
linear bulk viscosity #1 ......... = 6.0000E-02
stress rate option ............... = 1
eq.1: jaumann
eq.2: green-nagdi
eq.3: hyperelastic
g ................................ = 1.3300E+02
a ................................ = 1.1860E+00
b ................................ = 1.0570E+00
n ................................ = 6.1000E-01
c ................................ = 2.3000E-02
m ................................ = 6.0000E-01
melt temperature ................. = 1.7230E+03
room temperature ................. = 2.9300E+02
eps0 ............................. = 1.0000E-07
specific heat .................... = 1.1700E-04
pressure cutoff .................. = -1.0000E+30
spall type ....................... = 1.0000E+00
plastic strain iteration flag .... = 0.0000E+00
eff plastic strain at failure .... = 0.0000E+00
failure parameter option ......... = 0.0000E+00
eq.1 delete element when D > 1
d1 ............................... = 5.5000E+00
d2 ............................... = 0.0000E+00
d3 ............................... = 0.0000E+00
d4 ............................... = 0.0000E+00
d5 ............................... = 0.0000E+00
EQUATION OF STATE (volumetric behavior): This is linear polynomial
c0 ............................... = 0.0000E+00
c1 ............................... = 1.3800E+02
c2 ............................... = 0.0000E+00
c3 ............................... = 0.0000E+00
c4 ............................... = 0.0000E+00
c5 ............................... = 0.0000E+00
c6 ............................... = 0.0000E+00
e0 ............................... = 0.0000E+00
initial relative volume .......... = 1.0000E+00
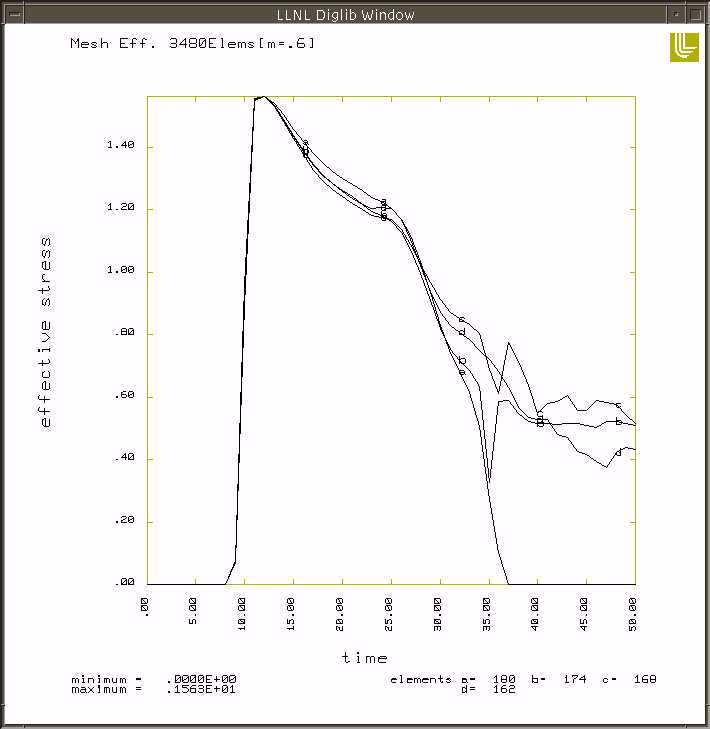
The following pictures are different areas and types of stresses for the 20m/s impact speed.
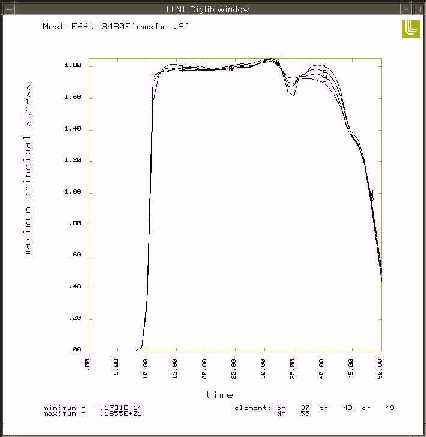
20 m/s von mises stress vs time
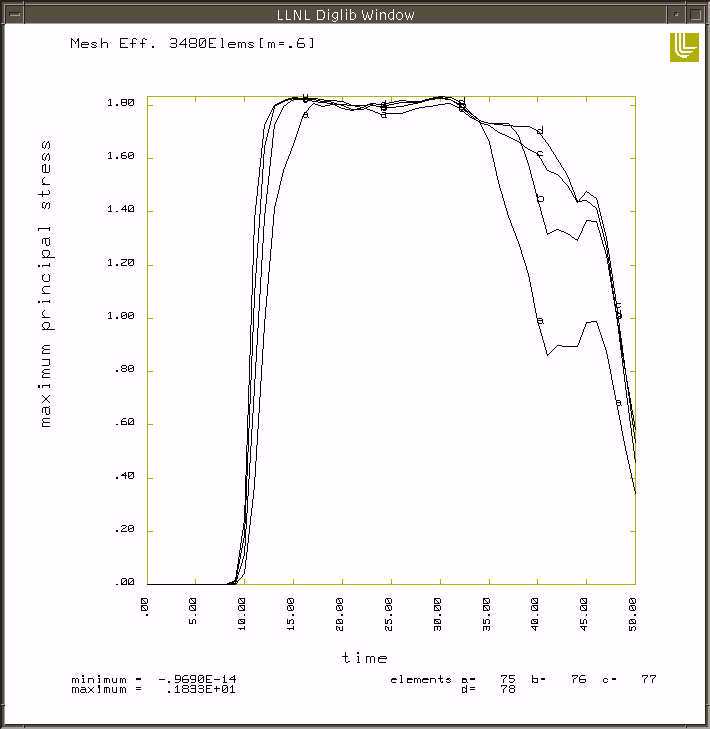
20 m/s maximum principal stress vs time
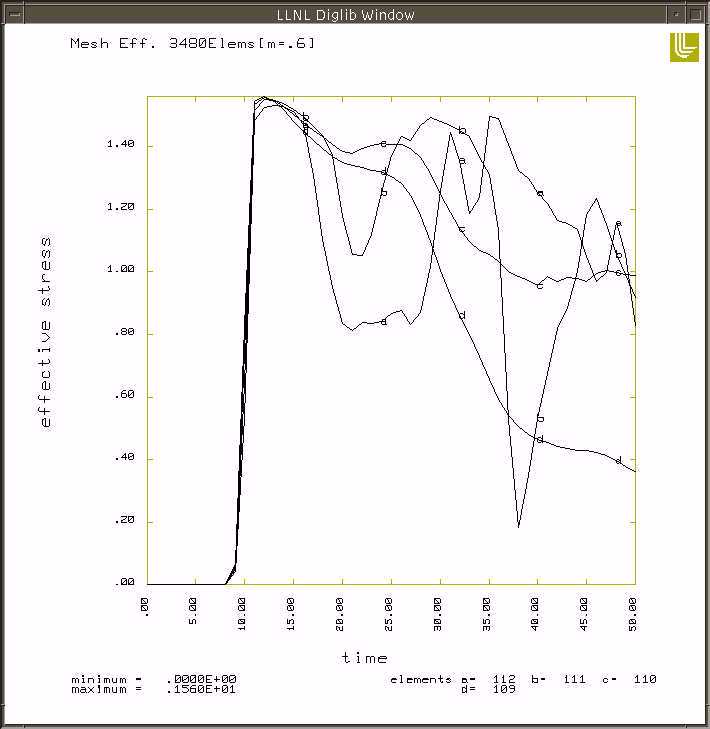
20 m/s von mises stress vs time
