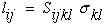 |
(26) |
Ronald D. Kriz, Associate Professor
Engineering Science and Mechanics
Virginia Polytechnic Institute and State University
Blacksburg, Virginia 24061
Another linear constitutive relationship, similar to equation (24), exists for compliances, Sijkl, that relate stresses with strains.
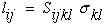 |
(26) |
Compliances like stiffnesses can be considered fourth order tensors because they transform as fourth order tensors.
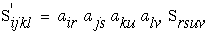 |
(27) |
Hence the relationship between compliances and stiffness can be shown as an inverse relationship. This inverse relationship is shown here in reduced contracted notation. NOTE: although these matrices are inversely related, Sij and Cij are not tensors quantities because they do not transform as second order tensors.
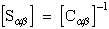 |
(28) |
Compliances, unlike stiffnesses, have a simple relationship with engineering elastic properties such as Young's modulus, shear modulus, and Poisson's ratio. For example the compliance along the z axis (3-direction), S33 is defined as the reciprocal of the Young's modulus in the same z-direction.
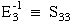 |
(29) |
Similarly expressions for shear modulus and Poisson's ratio in the y-z (2-3) plane can be simply derived from terms in the compliance matrix.
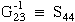 , , 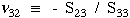 |
(30), (31) |
It is now possible to show how these three engineering elastic properties vary as a function of rotation from the z axes (3-direction) into the x-y (1-2) plane by using the general fourth order compliance tensor transformation of equation (27) where the direction cosine terms, aij, are expanded into sines and cosines of the rotation angle, q, starting at zero along the z axis and rotating 90o into the x-y plane. This transformation although simply done as a fourth order transformation, becomes a tedious task in reduced contracted notation. After much algebra the final equations are simplified, see Ref.[9].
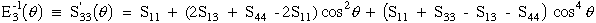 |
(32) |
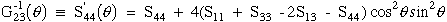 |
(33) |
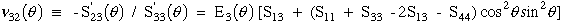 |
(34) |
For all isotropic engineering materials equations (32), (33), and (34) will, by definition, reveal no variation in properties as we rotate from the z axis into the x-y plane, hence circles in a two-dimensional (2-D) plane or spheres in a three-dimensional (3-D) space are visual representations (manifestations) of isotropic elastic properties. Unidirectional fiber-reinforced composite materials, on the other hand, exhibit highly ANisotropic behavior which is exhibited as significant deviations from the isotropic spherical geometry.
| Material | C33 | C11 | C12 | C13 | C44 | n32 | n12 |
|---|---|---|---|---|---|---|---|
| Epoxy-matrix (Kriz-Stinchcomb, 1979) | 8.63 | 8.63 | 4.73 | 4.73 | 1.95 | 0.345 | 0.345 |
| Carbon-fiber (Kriz-Stinchcomb, 1979) | 235 | 20.0 | 9.98 | 6.45 | 24.0 | 0.279 | 0.490 |
| Carbon-fiber (Dean-Truner, 1973) | 240 | 20.4 | 9.40 | 10.5 | 24.0 | 0.35 | 0.497 |
| Carbon-fiber (Smith, 1972) | 221 | 19.4 | 6.60 | 5.80 | 20.3 | 0.230 | 0.320 |
| Composite (60% Fiber) (Kriz-Stinchcomb), 1979) | 144 | 13.6 | 7.0 | 5.47 | 6.01 | 0.284 | 0.497 |
| Material |
Poisson's Ratio(n)
Modulus: Bulk(K), Shear(G), Young's(E) Subscripts: Matrix(m), Fiber-Axis(L), Transverse-Plane(T) |
||||
|---|---|---|---|---|---|
| Isotropic: two independent properties-> | Em | nm | |||
| Epoxy-matrix (Kriz-Stinchcomb, 1979) | 5.35 | 0.345 | |||
| Hexagonal: five independent properties-> | EL | ET | GLT | GTT | KTT |
| Carbon-fiber (Kriz-Stinchcomb, 1979) | 232 | 15.0 | 24.0 | 5.02 | 15.0 |
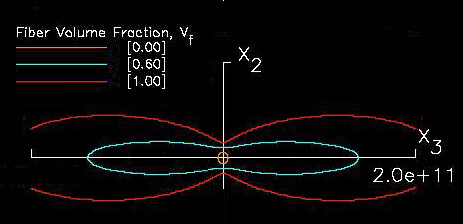
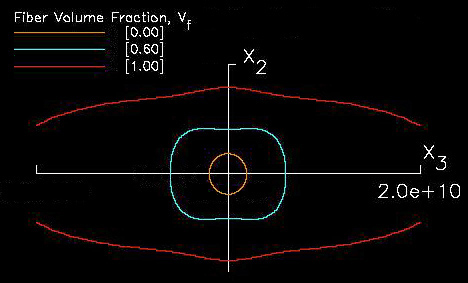
For example if we take elastic properties predicted in Ref.[10], see Table 1., for unidirectional carbon-fiber/epoxy composites and substitute these properties into equations (32), (33), and (34), both spherical and nonspherical geometries are predicted, see Figures 12, 13, and 14. In these figures the elastic properties are also shown as a function of fiber volume fraction where 0.0 fiber volume fraction yields pure isotropic epoxy properties, shown as circles, and 1.0 fiber volume yields pure anisotropic fiber properties and hence the geometry significantly deviates from the circular geometry. Even low fiber volume fractions yield significant anisotropy.
Click on image to start an interactive JWave session
Click on image to start an interactive JWave session
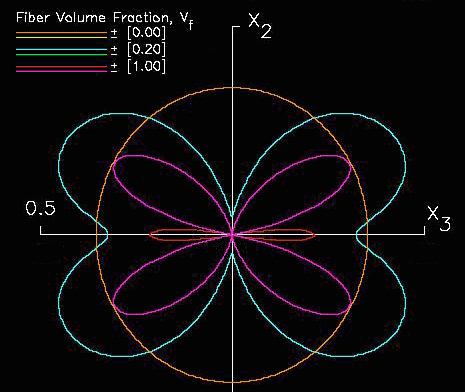
Figure 14. Polar diagram of graphite/epoxy Poisson's modulus n
32 for various fiber volume fractions, in GPa.
NOTE: yellow, green, and purple line indicates negative Poisson's ratio.
A closer look at these figures reveals some obvious facts, but also some unexpected new information. If all fibers are aligned along the z axis (3-direction) then we would expect that the elastic stiffness would be largest along the z axis (3-direction) and less stiff in the x-y (1-2) plane. Indeed this trend is confirmed geometrically. However unexpected properties are observed such as a large negative (-0.354) Poisson's ratio, see purple line in Figure 14. A negative Poisson's ratio would require that the material would expand both in the load direction and transverse direction to the load direction. If the material is transversely isotropic the transverse expansion would be the same in all directions within the transverse plane. Putting this all together would require that such a material when loaded in the fiber direction would expand in all directions, hence it's volume would increase under a uniaxial tension load.
Perhaps the reader might find other interesting mechanical behavior by experimenting with either the links to "Interactive JWave session" shown above each of the figures (12,13,14), or below an alternate link is provided that provides the student access to a more comprehensive interactive session with access to: (1) computer programs, (2) sample data files, (3) numerical results, and (4) images.
The elastic properties: Young's Modulus, E, shear modulus, G, and Poisson's Ratio, n, in each orthogonal plane can be used to classify the nine independent orthorhombic elastic constants in terms of engineering properties.
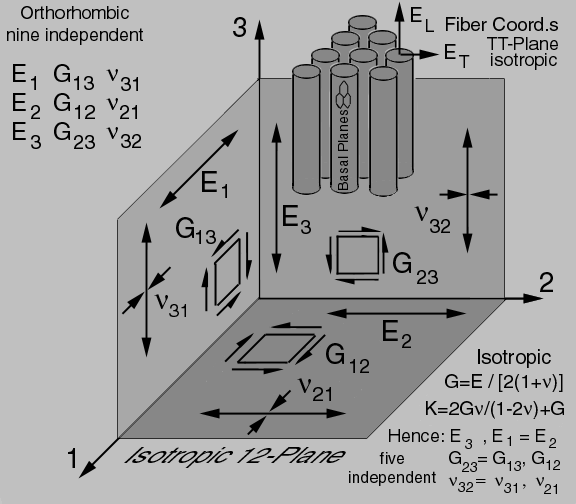
Figure 15. Transversely-isotropic carbon fibers and their composites.
With the mechanical behavior ("deformation") shown in each plane of Fig. 15 it is easier to see how each of these nine properties are independent. If all the fibers are aligned along the 3-axis, it is easy to see the 12-plane is transversely isotropic and the number of independent elastic properties reduce to 5 (hexagonal symmetry) and the isotropic relationships can be used in the 12-plane. The large negative Poisson's ratios predicted in Fig. 14 is most likely due to the nano-structure of the graphite fibers where basal planes become aligned parallel to the circumference when pyrolyzed. This pyrolyzation also creates a lamellar structure of basal planes aligned parallel to the fiber longitudinal axis ("L") and explains the unusually high elastic stiffness along the x3 axis. Together these two nano-structural observations explain the fiber has transversely- isotropic ("hexagonal") symmetry. Here we choose the fibers longitudinal axis to be parallel to the x3 axis because for hexagonal symmetry the x3 axis is the conventional "unique" symmetry axis. However in engineering design the x1 axis is the choosen as the fiber-axis convention.
A brief literature review has revealed some interested hypothetical structures for pyrolyzed carbon fiber structures, see Figure 16. Although preliminary observations can explain how this nano-structure results in a large modulus along longitudinal fiber axis, much more research needs to be done before we can conclude any nano-structure property relationship that can explain the large negative Poisson's ratios.
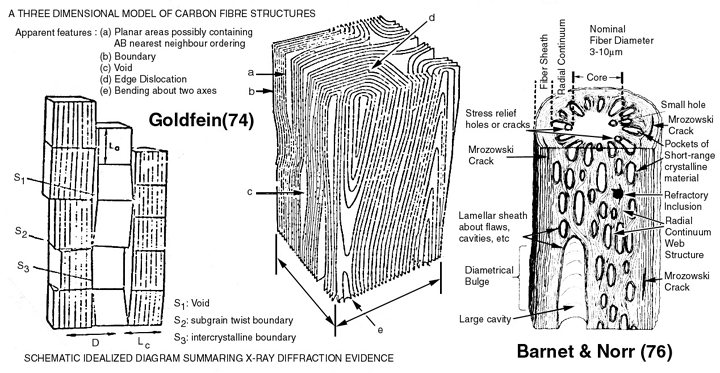
Figure 16. Carbon fiber pyrolyzed structures Ref.[11] and Ref.[12].
Because so little is known about these transversely isotropic ("hexagonal") fiber properties, engineering designers make some gross approximations. For example the five independent elastic properties shown in Fig. 15 are further reduced to four independent elastic properties by equating all three shear moduli and similarly all three Poisson's ratios are also equated.
These same fiber-reinforced materials and their peculiar anisotropies will be used in the next section on "Laminated Plate Theory". As a result we can expect some unusual mechanical behavior of laminated plates fabricated with these materials at the micro level.
Geometric representations of engineering elastic properties, E, G, n, although interesting, can only reveal variations of just that one property. The modulus E3 = S33-1 represents only one of nine components of a fourth order tensor and consequently does not represent the full anisotropy of all components of the stiffness tensor. Next we will show how to geometrically represent anisotropy that includes all possible terms (components) of the fourth order stiffness tensor.